浅谈排序算法

排序算法有很多种，今天先谈谈一些简单的排序算法。包括桶排序、冒泡排序和快速排序算法。后期总结各种排序算法。

桶排序（BucketSort）

排序过程：

假如我们现在要排序的一组数为：5,3,5,2,8. 这组数都在0-10的范围之内。这个时候，我们可以拿11个桶，标号为0,1,2,3……10。也就是定义长度为11的数组。现在我们来遍历这些数字，第一个数字为5，那么给第五号桶中插一个小红旗，第二个数字为3，给第三号桶插一个小红旗，以此类推。其中，插入一个小红旗代表的是数组元素+1（开始初始化数组元素都为0)，遍历完成之后，可以查看所有桶中小红旗的数量，也就是数组中存储元素的个数。发现a[5] = 2，表示5这个数字出现了两次。从0号桶开始，a[0] = 0,表示没有0这个数字，依次遍历到 10就结束了，也就把这些数字从小到大排好了。

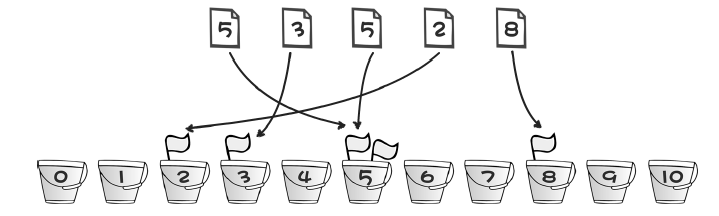
当然，如果需要对0-100之间的数进行排序，就需要101个桶，桶的作用就是一个标志。

把标志数组起个名字为book。

写代码思路：

1.把book数组初始化，也就是把里面都写成0

2.把需要排序的一组数放在一个数组里面。

3.循环放入的过程中，对book[i]++。

4.依次判断编号为0~10之间的桶中小红旗的个数，即book[i]的值

5.有n个小红旗（book[i] = n）就打印n次这个数。

代码如下：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
//桶排序：对于0~100之间的数排序的时候，这时候需要有101个桶（数组长度为101的数组），插个小旗（加一）用来标记每个数出现的次数。
//然后，看这些桶中（遍历这个数组）小旗的数目（多少个1），有多少只旗（多少个1）就（打印多少次这个数）表示这个桶的标号（数）出现了几次；
int main(){
	int book[11];//先拿11个桶，0~10之间的数进行排序。
	int t = 0;
	for (int i = 0; i < 11; i++)
	{
		book[i] = 0; //初始化数组（把桶清空）
	}
	int n = 0;//要对n个数排序
	printf("请输入需要对几个数进行排序：");
	scanf("%d", &n);//输入n个需要排序的数
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &t);//把数输入到t中
		book[t]++;       //进行计数，第t个桶插加一个旗
	}
	for (int i = 0; i < 11; i++)   //依此判断编号为0~10的桶，（从小到大）。
	{
		for (int j = 0; j < book[i]; j++) //出现几个就打印几次
		{
			printf("%d ", i);
		}
	}
	system("pause");
	return 0;
}

桶排序这种方法存在明显的问题就是占用了太多的空间。假如需要排列的数中有一个10000，那么最少得定义数组长度为10000的数组。

冒泡排序（BubbleSort）

冒泡排序的思想：

每次比较两个相邻的两个数，如果它们的顺序是错误的（要求是从小到大，此时的序列是前面的比后面的大）就把它们进行交换。如果有n个数进行排序，要进行n-1趟操作，而每一趟比较都要从第一个数开始，两两进行比较，将较大的数，放在后面。重复此步骤直到最后一个尚未归位的数，已经归位的数则无需比较。

排序过程：

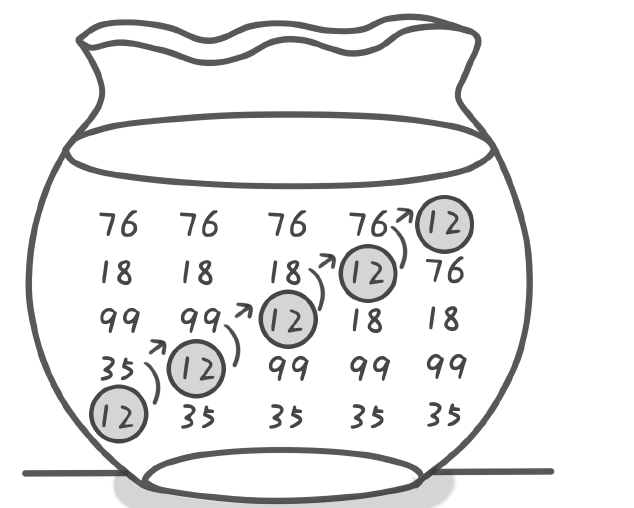
假设我们现在对12,35,99,18,76这几个数由大到小进行排序。也就是前面的数比后面的大。

把1个位归位成为跑一趟

第一趟：

首先，比较12和35，发现12小于35，那么要交换这两个数。得到35,12,99,18,76.

然后，继续比较第二位和第三位，发现12比99小，交换得到，35,99,12,18,76.

接着，比较第三位和第四位，发现12小于18，交换得到，35,99,18,12,76.

最后，比较第四位和第五位，发现12小于76，交换得到，35,99,18,76,12.

四次比较后，发现最小的数12已经归位。然而这还只是把1个数归位了。接下来归位剩余的四个数。

第二趟：

现在归位第次小的数，跟第一趟过程差不多。

首先，比较35和99，发现小，那么交换之，得到99,35,18,76,12.

···

因为12已经归位了，所以没有必要比较第四位和第五位的大小。

…

这趟完成后，次小的数也已经归位了

第三趟：

···

第四趟：

···

直到得到最后的序列

排序的原理：

如果有n 个数进行排序，只需将n-1 个数归位，也就是说要进行n-1 趟操作。而“每一趟”都需要从第1 位开始进行相邻两个数的比较，将较小的一个数放在后面，比较完毕后向后挪一位继续比较下面两个相邻数的大小，重复此步骤，直到最后一个尚未归位的数，已经归位的数则无需再进行比较.

代码描述：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>

int main()
{
	int arr[100];
	int n = 0;//需要对n个数进行排序(从小到大)
	int temp = 0;
	printf("请输入需要对几个数进行排序:");
	scanf("%d", &n);
	for (int i = 0; i < n; i++){
		scanf("%d", &arr[i]);
	}

	//冒泡排序:

	//先分开写：
	////第一趟：
	//for (int i = 0; i < n -1; i++)
	//{
	//	if (arr[i]>arr[i + 1]){
	//		temp = arr[i];
	//		arr[i] = arr[i + 1];
	//		arr[i + 1] = temp;
	//	}
	//}
	////第二趟：
	//for (int i = 0; i < n - 2; i++)
	//{
	//	if (arr[i]>arr[i + 1]){
	//		temp = arr[i];
	//		arr[i] = arr[i + 1];
	//		arr[i + 1] = temp;
	//	}
	//}
	////需要 n-1 趟
	////...
	
	
	//合并起来：
	for (int times = 1; times <= n - 1; times++){
		for (int i = 0; i < n - times; i++){
			if (arr[i]>arr[i + 1]){
				temp = arr[i]; //交换的过程
				arr[i] = arr[i+1];
				arr[i+1] = temp;
			}
		}
	}

	//打印排好序的数组
	for (int i = 0; i < n; i++)
	{
		printf("%d ", arr[i]);
	}
	system("pause");
	return 0;
}

快速排序（QuickSort）

快速排序的过程：

我们对需要排序的序列6 1 2 7 9 3 4 5 10 8 ，首先在这组数中找一个基准数，我们就把第一个数6作为基准数，接下来，需要将这个序列中所有比基准数大的数放在6 的右边，比基准数小的数放在6 的左边。

分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6 的数，再从左往右找一个大于6 的数，然后交换它们。这里可以用两个 变量i 和j，分别指向序列最左边和最右边。

其实哨兵j 的使命就是要找小于基准数的数，而哨兵i 的使命就是要找大于基准数的数，直到i 和j 碰头为止。

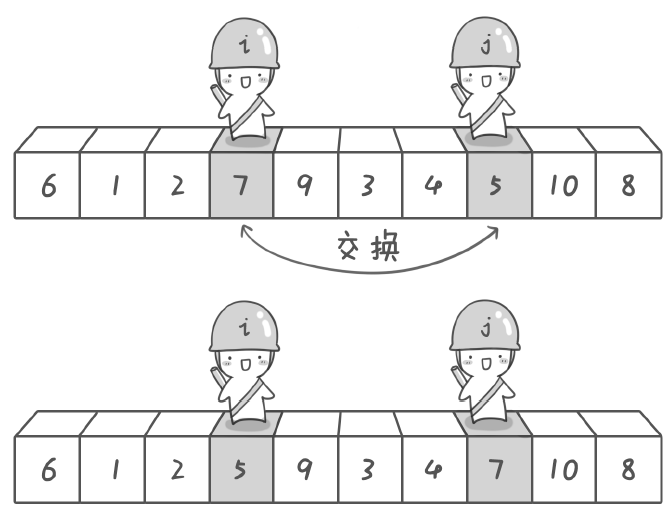
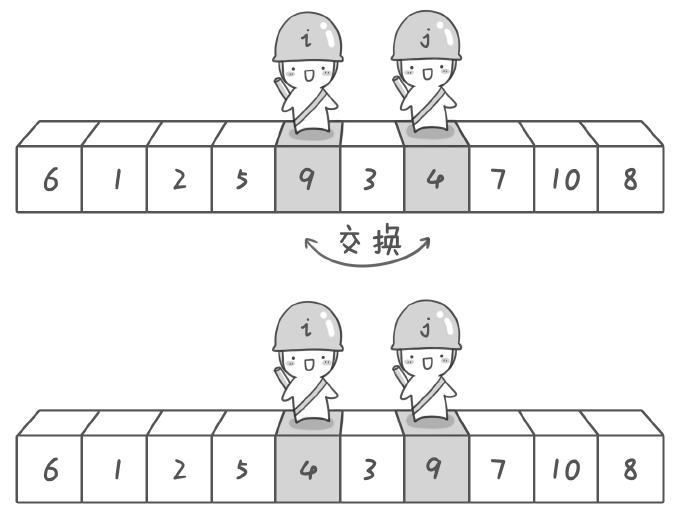
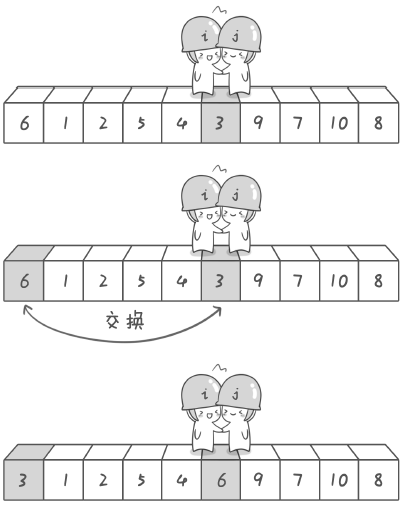
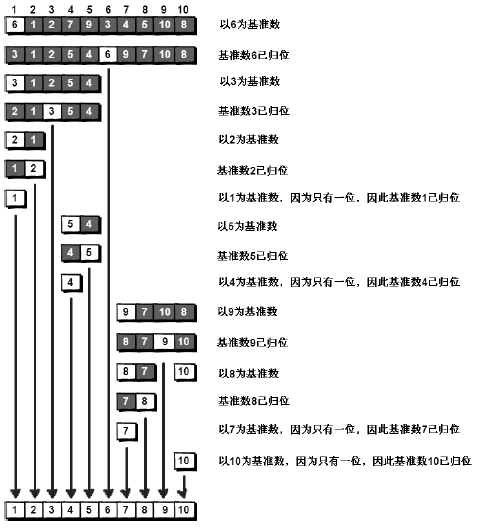
此时，基准数6已经归位，左边的序列是3 1 2 5 4 右边的是 9 7 10 8 ，接下来分别处理这两个序列。处理方法跟上述类似。

其实快速排序的每一轮处理都是将这一轮的基准数归位，直到所有的数归位为止。

代码流程：

1.将需要排序的序列放在一个数组中调用排序算法

2.设置哨兵i和j和基准数。

3.哨兵j先走，哨兵j找出小于基准数的值，哨兵i找出大于基准数的数。

4.若i和j没要到则交换这两个数。反之，将基准数归位，即交换arr[i]和基准数。

5.一轮完成后，剩下的就是将左边后右边的序列进行递归调用快速排序方法，直到将所有子序列排列完成为止。

6.输出排好序的数组

代码实现：

#include <stdio.h>
#include <stdlib.h>
//分别从初始序列“6 1 2 7 9 3 4 5 10 8”两端开始“探测”。先从右往左找一个小于6 的数，再从左往右找一个大于6 的数，然后交换它们。这里可以用两个
//变量i 和j，分别指向序列最左边和最右边。

//其实哨兵j 的使命就是要找小于基准数的数，而哨兵i 的使命就是要找大于基准数的数，直到i 和j 碰头为止。

/*快速排序的每一轮处理其实就是将这
一轮的基准数归位，直到所有的数都归位为止，排序就结束了。
*/
void qSort(int left, int right,int arr[])
{
	int i, j, temp, basic;
	if (left > right)
		return;
	i = left;    //哨兵i和j分别指向left和right
	j = right;
	basic = arr[left];//基准数
	while (i != j){
		//哨兵j先走，要有顺序，因为此处设置的基准数是最左边的数
		while (arr[j] >= basic && i < j){//哨兵j的使命就是找出小于基准数的数
			j--;
		}
		while (arr[i] <= basic && i < j){//哨兵i的使命就是找出大于基准数的数
			i++;
		}
		//i和j没遇到，交换着两个值
		if (i < j){
			temp = arr[i];
			arr[i] = arr[j];
			arr[j] = temp;
		}
	}
	//i和j相遇，将基准值归位.
	//上面有了代码 basic = arr[left]  ，basic这时候就是一个临时变量
	arr[left] = arr[i];
	arr[i] = basic;

	//把基准值归位后就进行 基准值左边和基准值右边部分 的 递归排序
	qSort(left, i - 1, arr);
	qSort(i + 1, right, arr);
}
int main(){
	int arr[] = {6,1,2,7,9,3,4,5,10,8};
	qSort(0,9,arr);
	for (int i = 0; i < 10; i++)
	{
		printf("%d ", arr[i]);
	}
	system("pause");
	return 0;
}

参考书

《啊哈！算法》